我中心在图迁移学习和微分方程问题求解等领域取得新进展，相关成果被IJCAI2025接收

第34届IJCAI（International Joint Conference on Artificial Intelligence）于2025年8月16日至8月22日在加拿大蒙特利尔召开，卫星会议于8月28日至8月31日在广州召开。我中心2024级硕士生马鑫、2023级硕士生黄睿的两篇论文被 IJCAI 2025接收，并进行现场汇报。IJCAI是人工智能领域国际顶级会议，IJCAI 2025共收到5404篇投稿，录用率为19.3%。

论文1：《PALA: Class-imbalanced Graph Domain Adaptation via Prototype-anchored Learning and Alignment》（2024级研究生马鑫为共同一作，琚玮副研究员和我中心主任吕建成教授为通讯作者）。

背景：作为图迁移学习的一个分支，无监督图域自适应旨在促进从带有丰富标签的源域图到无标签目标域图的知识迁移。然而，大多数现有研究都假设源图中的标签分布是均衡的，但这一假设在许多真实场景中并不成立。这会带来关键挑战：源图知识存在偏差，并且域间存在严重的分布差异。考虑到类别原型在表征域语义上的优势，本文提出了一种基于原型锚定学习与对齐的类不平衡图域自适应框架。

图1 论文poster展示

方法与创新：我们是首个专门针对类不平衡的图域自适应的工作。在我们的工作中，我们提出了一种基于原型锚定的学习与再校准策略，以消除源图中的原型偏差，并设计了一种新颖的对比学习原型对齐方法。具体一点，为了消除源图中的类别不平衡带来的知识偏差，我们设计了基于原型锚定的学习和再校准模块，通过线性组合的方式为每一个查询实例构建基于可学习原型以及错误分类集合的正负样本用于对比学习，同时为每一个原型计算对应的校准因子用于对原型由于类别不平衡带来的潜在偏差进行校准；为了将知识从源域迁移到目标域，我们设计了基于原型的对比学习模块，采用自监督的标记策略为每一个目标域实例生成伪标签，然后在源域和目标域之间进行加权的对比学习进行对齐，以捕获域不变性知识，实现知识的迁移。

实验验证：在多个广泛使用的标准数据集上的实验表示，我们提出的方法优于诸多基准方法。

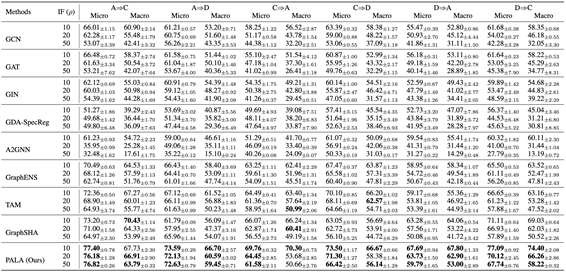
图2 PALA在多个基准数据集上的表现。

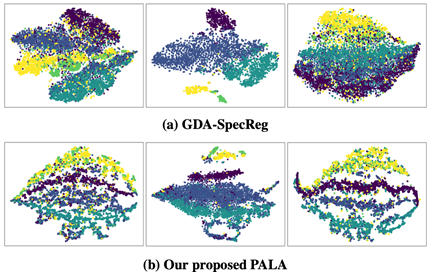
图3 PALA和基准方法学习到的节点表示的t-SNE可视化对比。

总结：在本文中，我们关注图数据中普遍存在的类不平衡特性，并提出了一种新颖的基于原型锚定的学习与对齐框架 PALA，用于解决类不平衡图域自适应问题。在多个公开数据集上的大量实验表明，我们的方法在处理类不平衡图域自适应方面具有显著优势。

论文2：《DONIS: Importance Sampling for Training Physics-Informed DeepONet》（黄树东副研究员为该论文第一作者、冯文韬副教授为该论文唯一通讯作者、硕士研究生黄睿为第二作者，其他作者包括我中心主任吕建成教授、2023级硕士研究生胡明）。

图4 论文现场汇报展示

背景：
DeepONet 能有效学习复杂的算子映射，在求解微分方程问题中表现出色。其扩展版本 PI-DeepONet 进一步引入物理约束，在无监督或弱监督情境下也能获得良好性能。然而，物理约束与算子学习的结合显著提升了训练过程的计算复杂度，尤其在处理非线性或高维问题时，训练困难和收敛缓慢成为主要瓶颈。

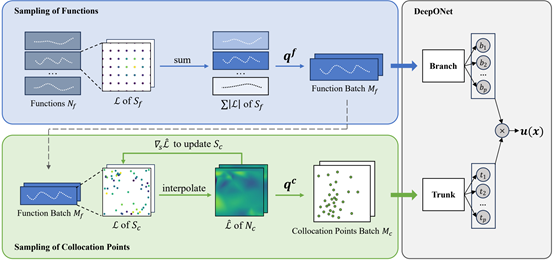
图5 本文提出的DONIS模型的整体架构。

方法：
为提升训练效率，本文提出了一种实用且通用的加速框架：DONIS（PI-DeepONet with Importance Sampling）。该方法利用 DeepONet 架构的灵活性，设计了一个双阶段重要性采样机制，分别针对输入函数和配点（collocation points）进行采样优化。其中，对函数输入采用简易实现的采样策略，对配点则引入基于空间梯度的影响力估计，从而优先选取对目标学习贡献更大的样本，提高训练效率与预测精度。

实验：
本文方法在 Allen-Cahn 方程、粘性Burgers方程和非线性扩散-反应方程三个典型 PDE 任务上进行了验证。实验结果显示，所提方法在保持物理一致性的同时，相较原始 PI-DeepONet 在收敛速度和预测精度上均有明显提升。

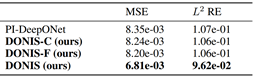
图6 Allen-Cahn equation实验结果。

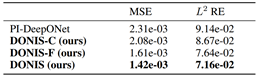
图7 Burgers’ equation实验结果。

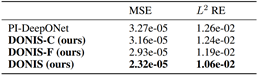
图8 nonlinear diffusion-reaction equation实验结果。

总结：
本文提出的 DONIS 框架通过双阶段重要性采样策略，显著提升了 PI-DeepONet 在求解复杂微分方程中的训练效率与预测精度。得益于 DeepONet 架构的灵活性和方法设计的模块化，DONIS 具有良好的泛化能力，可适配多种不同类型的 PDE 问题，尤其在无监督和弱监督场景。